3004. Queue
At a railway
station, there are k ticket counters, but only a single queue leading to
them. The service process works as follows:
Initially, when
all counters are free, the first k people from the queue go to the
counters. The remaining customers wait in line. As soon as a counter becomes
available after serving a customer, the next person in the queue takes the
vacant spot. This process continues until all customers have been served.
Determine the time
required to serve all customers.
Input. The first line
contains two integers: the size of the queue n and the number of ticket counters k (1 ≤ n
≤ 105, 1 ≤ k
≤ 104).
The second line contains n
positive integers ti (1 ≤ ti ≤ 105) – the service time for
the i-th customer.
Output. Print one integer
– the minimum
time required to serve the entire queue.
|
Sample
input |
Sample
output |
|
7 3 1 2 3 4 5 3
1 |
7 |
SOLUTION
set
Algorithm analysis
Let’s simulate the ticket-selling process using a multiset s.
First, assign the first k people to the available counters and record
their service times in the multiset.
During the process, the multiset will always contain k
elements, each representing the moment when a corresponding counter becomes
available to serve the next customer. Clearly, each new person should go to the counter with the
earliest available time.
The service time of the last customer will be the desired
result.
Example
Let’s consider the given
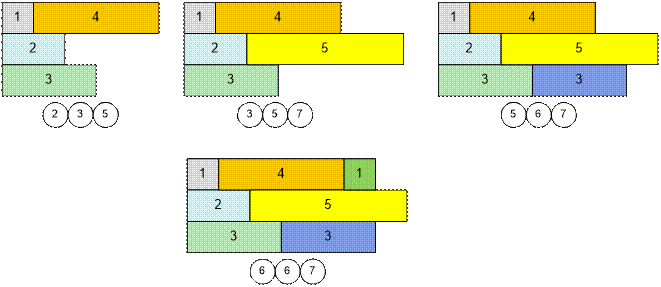
example. First, add the first k = 3 elements to the heap.
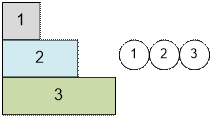
At each
iteration, take the next element (the next person in the queue) and place him
in the position of the smallest value – at the counter that will become
available first. Add to the queue the time when this new person will finish his
service at the counter.
Next to each
illustration, the numbers in the heap are shown.
Algorithm implementation
Store the timestamps of ticket sales at the counters in the multiset s.
multiset<long
long> s;
Read the input data. The service times of the first k people are added to s.
scanf("%d
%d",&n,&k);
for
(i = 0; i < n; i++)
{
scanf("%d",&ti);
if (s.size() != k) s.insert(ti);
else
{
Find the
person who will finish his service first and place the next person in line
after them.
long long
temp = *s.begin();
s.erase(s.begin());
s.insert(temp + ti);
}
}
The largest number in the multiset s represents the moment when the
last customer will be served. This is the desired result.
while
(s.size() > 1) s.erase(s.begin());
printf("%lld\n",*s.begin());
Algorithm implementation – priority queue
Create a heap, which root contains the smallest
element.
priority_queue<long long, vector<long long>,
greater<long long>
> pq;
Read the input data. Put the service time of the first k people into the queue pq.
scanf("%d
%d",&n,&k);
for
(i = 0; i < n; i++)
{
scanf("%d",&ti);
if (pq.size() != k) pq.push(ti);
else
{
Find the
person who will finish his service first and place the next person in line
after them.
long long
temp = pq.top(); pq.pop();
pq.push(temp + ti);
}
}
The largest number in the priority queue pq represents the moment
when the last customer will be served. This is the desired result.
while
(pq.size() > 1) pq.pop();
printf("%lld\n",pq.top());
Java implementation
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int k = con.nextInt();
PriorityQueue<Long> pq = new
PriorityQueue<Long>();
for(int i = 0; i < n; i++)
{
long ti = con.nextLong();
if (pq.size() != k) pq.add(ti);
else pq.add(pq.poll() + ti);
}
while(pq.size() > 1) pq.poll();
System.out.println(pq.poll());
}
}